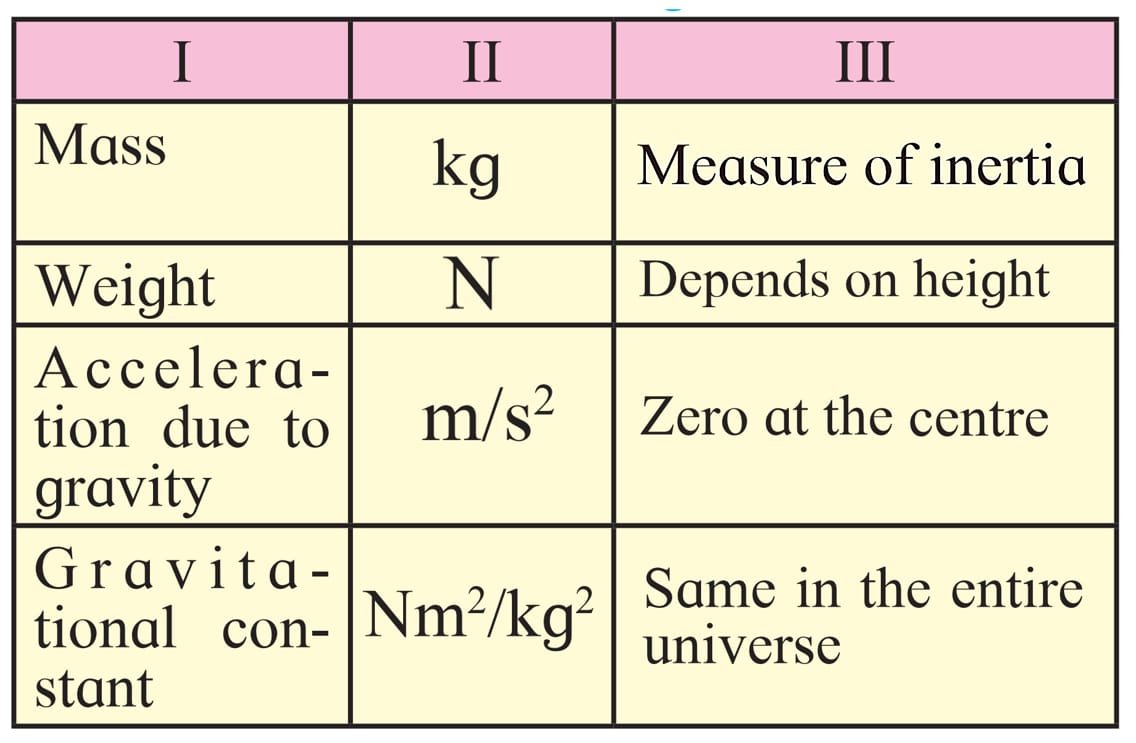
1. Study the entries in the following table and rewrite them
putting the connected items in a single row.
GRAVITATION EXERCISE QUESTIONS
2. Answer the following questions.
a. What is the difference between mass and weight of an object.
Will the mass and weight of an object on the earth be same as
their values on Mars? Why?
Mass –
– It is the amount of matter present in an object.
– Its value remains same everywhere.
– It can never be zero
Weight –
– It is the force with which the earth attracts an object.
– It keeps changing from place to place.
– It becomes zero at the Centre of earth
It is the product of mass and gravitational acceleration,
i.e., W = F = mg
Hence, the mass of an object on earth will be same as its value
on Mars.
As the weight depends on the value of acceleration due to
gravity (g) which changes from place-to-place, and is different
for earth and Mars, the weight of the object on earth will be
different than its value on Mars.
b. What are (i) free fall, (ii) acceleration due to gravity (iii)
escape velocity (iv) centripetal force?
Free fall:
The motion of any object under the influence of the force of
gravity alone is called as free fall.
Acceleration due to gravity:
The acceleration produced in a body under the influence of the
force of gravity alone is called acceleration due to gravity.
Escape velocity:
The minimum velocity with which a body should be projected
from the surface of a planet or moon, so that it escapes from the
gravitational influence of the planet or moon is called as escape
velocity.
Centripetal force:
The force acting on any object moving in a circle and directed
towards the centre of the circle is called as centripetal force.
c. Write the three laws given by Kepler. How did they help
Newton to arrive at the inverse square law of gravity?
(i) Kepler’s first law: The orbit of a planet is an ellipse with the
Sun at one of the foci.
(ii) Kepler’s second law: The line joining the planet and the Sun
sweeps equal areas in equal intervals of time.
(iii) Kepler’s third law: The square of its period of revolution
around the Sun is directly proportional to the cube of the mean
distance of a planet from the Sun.
Centripetal force (F) acting on a planet of mass ‘m’ and velocity
‘v’, revolving at a distance of r from the sun is given as,
F= mv2 / r … (i)
When a planet is moving around the sun, Distance travelled by
planet in one revolution = Circumference of orbit = 2πr
Time period of revolution = (T)
∴ speed of planet v = distance / time
V = 2πr / T … (ii)
Substituting eq. (ii) in (i)
∴ F = m (2πr / T )2 / r = m4π2r2 / rT2
∴ F = 4mπ2r / T2
Multiplying numerator and deno
Multiplying numerator and denominator with ‘r2’.
∴ F = 4mπ2r / T2 × r2 / r2
∴ F = 4mπ2r3/ r2T2 … (iii)
According to Kepler’s 3rd law
T2 / r3 = k or r3/ T2 = 1/k … (iv)
Substituting (iv) in (iii)
F = 4mπ2r3 / r2T2 × 1/ k = 4mπ2 / r2k …(v)
Rearranging eq. (v)
F = 4mπ2 / k × 1 / r2
Since 4mπ2 / k = constant.
∴ F = constant × 1/ r2
∴ F α 1/r2
Thus, Newton concluded that, centripetal force is responsible
for circular motion of the planet and this force is inversely
proportional to square of distance between planet and sun.
GRAVITATION EXERCISE QUESTIONS
e. If the value of g suddenly becomes twice its value, it will
become two times more difficult to pull a heavy object along
the floor. Why?
The weight of an object is defined as the force with which the
earth attracts the object. This force is given as –
W = F = mg
The weight of an object depends on the mass of the object and
the value of acceleration due to gravity.
If the value of g doubles, the force with which the earth attracts
the object also becomes twice. Thus, the object becomes twice
as heavier, making it harder to be pulled along the floor.
GRAVITATION EXERCISE QUESTIONS
3. Explain why the value of g is zero at the centre of the earth.
The acceleration due to gravity (g) on earth’s surface is given
as,
G = GM / R2
The value of g depends on the mass M of the earth and the
radius R of the earth.
As we go inside the earth, our distance from the centre of the
earth decreases and no longer remains equal to the radius of
the earth (R).
Along-with the distance, the part of the earth which contributes
towards the gravitational force felt also decreases, decreasing
the value of (M).
Due to combined result of change in R and M, value of g
becomes zero at the centre of the earth.
GRAVITATION EXERCISE QUESTIONS
4. Let the period of revolution of a planet at a distance R from
a star be T. Prove that if it was at a distance of 2R from the
star, its period of revolution will be 8√ T.
According to Kepler’s third law, the square of orbital period of
revolution T of a planet around a star is directly proportional to
the cube of the mean distance R of the planet from the star.
T 2 α R 3
T 2 = k (R)3 …. (1)
Where, k is constant of proportionality.
When the planet is at a distance of 2R from the star, then its
period of revolution T’ will be,
T’ 2 α (2R)3
T’ 2 = k (2R)3 …. (2)
Dividing equations (1) and (2), we get,
T 2 / T’2 = (R) 3 / (2R) 3
T 2 / T’2 = 1/ 8
T’2 = √8 T
Thus, for a planet at a distance of 2R from the star, its period of
revolution will be √8 T
